Esperienze di Fisica
In questa pagina presentiamo
- i requisiti teorici di alcuni moti oscillatori smorzati soggetti ad attriti di carattere viscoso e radente e le corrispondenti equazioni differenziali
e nella successiva
- l'esperienza svolta in un laboratorio di fisica scolastico, la relativa elaborazione e il confronto con una simulazione numerica.
Studio di moti oscillatori smorzati
Introduzione
I moti oscillatori rappresentano una parte importante dello studio in fisica e permettono di comprendere il comportamento di molti sistemi naturali semplici e/o complessi quali, per esempio, l'oscillazione di un pendolo, le vibrazioni di
una corda tesa, il suono di un diapason ma pure la nota di uno strumento musicale, le vibrazioni di una molecola... . I sistemi più semplici rappresentati dalle oscillazioni di una massa appesa ad una molla o quelle di piccola
ampiezza di un pendolo si affrontano comunemente già a livello elementare e offrono al docente ottime occasioni per uno studio sperimentale. Non appena poi si disponga di adeguate conoscenze sulle equazioni differenziali e quindi
nell'ultimo anno di scuola superiore, se ne può dedurre anche la soluzione generale.
D'altra parte un grave appeso ad una fune e spostato dalla sua posizione di equilibrio così come un'altalena lasciata oscillare liberamente, mostrano sì un moto oscillatorio ma con una ampiezza che gradualmente diminuisce e
alla fine, immancabilmente, tali sistemi "convergono" alla condizione di equilibrio e si fermano. Il motivo di tale comportamento è dovuto alle forze di attrito che, manifestamente non conservative, implicano quindi una dissipazione
di energia. Benché tali moti appaiano più realistici di un moto armonico di ampiezza costante, ciò nonostante ci si concentra normalmente sui sistemi più semplici date le difficoltà di una analisi teorica
adeguata per questi moti oscillatori.
Nelle due pagine in cui si articola questa proposta didattica intendiamo invece studiare tali sistemi "complessi", dapprima con
- una analisi teorica comprensibile a studenti del quinto anno; successivamente presentiamo
- un'esperienza di laboratorio che permetta una buona riproducibilità del moto oscillatoro smorzato di un corpo rigido; infine procediamo ad una
- elaborazione dei dati raccolti con metodi numerici utilizzando un comune foglio di calcolo.
Poiché l'elaborazione numerica procede con ipotesi e relazioni relativamente semplici, la parte teorica non costituisce un prerequisito essenziale per la seconda e per tale motivo la si sviluppa
in questa pagina separata.
Parallelamente all'elaborazione su foglio di calcolo dove si riportano i risultati di quattro prove, si affianca e si distribuisce un notebook di Mathematica con il quale si
sono elaborate diverse altre prove, specie nella fase di messa a punto complessiva dell'esperienza.
Infine si propone una breve bibliografia di testi e articoli consultati.
Analisi teorica in presenza di attrito
Attrito viscoso
Il sistema costituito da una massa, generalmente piccola così da considerarla puntiforme appesa ad una fune e libera di oscillare permette l'applicazione delle leggi della dinamica del punto. Diversamente il pendolo composto o
pendolo fisico è invece costituito da una massa distribuita su un corpo rigido e oscillante in un moto piano attorno ad un asse fisso. Per il suo studio sono necessarie le leggi della dinamica che coinvolgono grandezze quali
il momento torcente e il momento di inerzia del corpo.
Consideriamo pertanto un corpo rigido di forma rettangolare di lunghezza \(L\) e massa \(m\), libero di ruotare attorno ad un asse orizzontale passante per \(O\) e sia \(h\) la
distanza tra il punto di sospensione \(O\) e il baricentro o centro di massa \(G\) (figura 1).
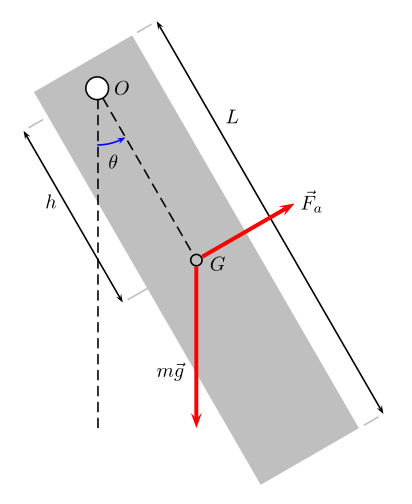
Le forze agenti su tale corpo sono evidentemente la forza peso \(m\vec{g}\) e le forze d'attrito dovute al moto in aria o in altro fluido del corpo e a quelle agenti sull'asse di rotazione.
A prescindere dalla forza peso certamente ben
nota allo studente, le forze d'attrito che lo studente generalmente incontra nel suo studio sono principalmente di due tipi: il primo, e maggiormente conosciuto, considera quelle forze dovute al moto relativo di corpi a contatto attraverso
le loro superfici. Sono le forze di attrito radente che, durante il moto, pur opponendosi alla velocità, rimangono sostanzialmente costanti e quindi indipendenti da questa. Vi sono invece le forze di attrito viscoso dovute al moto di
un corpo in un fluido che, diversamente, dipendono in misura anche complicata dalla velocità del corpo e quindi meno note allo studente. Tipici esempi riportati nei testi sono la caduta di un corpo in aria (paracadutista) o il moto
di un veicolo. L'analisi teorica che segue parte da queste ultime forze e ipotizza che queste dipendano proporzionalmente dalla velocità ossia si possano descrivere tramite la relazione vettoriale \(\vec{F}_a=-k\vec{v}\).
Se quindi \(\theta\) è l'angolo (o elongazione) che la verticale forma con la semiretta \(OG\), supposto positivo se antiorario a partire dalla verticale (figura 1), e \(I_O\) rappresenta il momento di
inerzia del corpo rispetto al polo \(O\), la seconda legge della dinamica per i corpi rigidi permette di scrivere l'equazione del moto
\begin{equation}
I_O\frac{\vec{d^2\theta}}{dt^2}= \vec{OG}\times (m\vec{g})+\vec{OG}\times \vec{F}_a. \label{eq:eq1}
\end{equation}
oppure, in alternativa,
\begin{equation}
I_O\,\vec{\alpha}= \vec{OG}\times (m\vec{g})+\vec{OG}\times (-k\vec{v}). \label{eq:eq02}
\end{equation}
dove \(\vec{\alpha}={\vec{d^2\theta}/dt^2}\) è il vettore dell'accelerazione angolare mentre a secondo membro compare la somma dei momenti torcenti dovuti al peso \(\vec{OG}\times (m\vec{g})\) e alla forza di attrito viscoso
\(\vec{OG}\times (-k\vec{v})\).
Se ora colleghiamo la velocità lineare del baricentro \(v\) a quella angolare \(\omega=d\theta/dt\) ponendo \(v=h\omega=h\,d\theta/dt\) e riportiamo la precedente alla forma scalare, otteniamo
Supposto il parametro \(k\gt 0\), controlliamo innanzitutto la coerenza di tale inserzione riferendoci alla figura seguente.
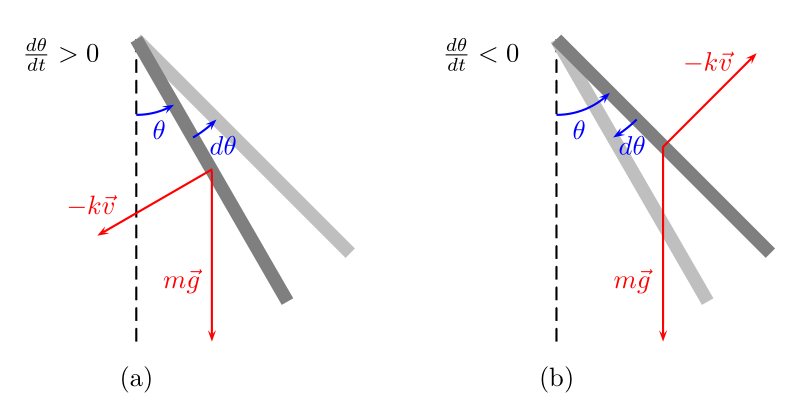
Difatti, nel caso che il corpo si stia allontanando dalla verticale ossia l'angolo \(\theta\) stia aumentando (caso (a)), la sua derivata è positiva e il momento torcente dovuto all'attrito viscoso possiede una componente negativa e quindi concorde al momento della forza peso. Se invece l'angolo \(\theta\) diminuisce per cui il corpo si sta avvicinando alla verticale e \(d\theta/dt \lt 0\) (caso (b)) e il momento torcente di tale attrito è correttamente opposto a quello del peso. In sostanza il segno della velocità angolare assicura il corretto verso del corrispondente momento torcente.
Riscritta la precedente come \begin{equation} \frac{d^2\theta}{dt^2}= -\frac{mgh}{I_O}\sin\theta -\biggl(\frac{kh^2}{I_O}\biggr)\frac{d\theta}{dt} \end{equation} determiniamo il momento d'inerzia \(I_O\). Poiché utilizziamo come corpo rigido una piccola asta in alluminio, il suo momento d'inerzia rispetto al baricentro \(G\) è \(I_G=1/12 mL^2\) (figura 1) ma essendo l'asse di rotazione a distanza \(h\), in base al teorema di Huygens-Steiner risulta \begin{equation} I_O=mh^2+I_G= mh^2+\frac{1}{12}mL^2=m\biggl(h^2+ \frac{1}{12}L^2\biggr) \end{equation} per cui in definitiva otteniamo \begin{equation} \frac{d^2\theta}{dt^2}=-\frac{gh}{h^2+L^2/12}\sin\theta-\biggl[\frac{kh^2}{m(h^2+L^2/12)}\biggr]\frac{d\theta}{dt}.\label{eq:eq06} \end{equation} Per preparare quest'ultima relazione allo studio numerico che intendiamo proporre, notiamo che la grandezza \((h^2+L^2/12)/h\) che compare a fattore del \(\sin(\theta)\) ha le dimensioni di una lunghezza per cui definiamo una lunghezza "efficace" \begin{equation} l_{eff}=\frac{h^2+L^2/12}{h},\label{eq:eq07} \end{equation} così come ridefiniamo il coefficiente della velocità angolare \begin{equation} b= \frac{kh^2}{m(h^2+L^2/12)}. \end{equation} Riprese inoltre le definizioni di velocità e accelerazione angolare \begin{equation} \omega= \frac{d\theta}{dt},\qquad \alpha= \frac{d^2\theta}{dt^2}, \end{equation} l'equazione \eqref{eq:eq06} si semplifica in \begin{equation}\bbox[border:1px solid red,15px,#ffffcc] {\alpha= -\frac{g}{l_{eff}}\sin\theta -b\,\omega.}\label{eq:eq10} \end{equation}
Partiremo da quest'ultima relazione per avviare la sua soluzione numerica.
Attrito radente
Nel caso sia presente una forza di attrito radente sappiamo che questa possiede verso opposto alla velocità ma che, diversamente dall'attrito viscoso, il suo modulo è indipendente dalla velocità. Dovremo quindi modificare la legge del moto \eqref{eq:eq02} sostituendo al termine proporzionale alla velocità un termine \(\vec{F}\) in modulo costante ma che sia comunque tale da opporsi al verso della velocità. Riprendendo quindi quanto detto circa la correttezza del segno reinterpretiamo nella figura 2 la forza d'attrito come un forza \(F\) di modulo costante: l'equazione del moto \eqref{eq:eq03} nel caso (a) di aumento dell'angolo \(\theta\) diviene in termini scalari,
\begin{equation} I_O\alpha= -mgh\sin\theta -hF\qquad\hbox{se}\qquad \frac{d\theta}{dt} \gt 0 \end{equation}in quanto il momento torcente della forza d'attrito agisce nello stesso verso di quello della forza peso. Nel caso (b) di figura 2 invece, dove l'angolo \(\theta\) sta diminuendo, il momento dovrà essere opposto a quello del peso per cui l'equazione diventa
\begin{equation} I_O\alpha= -mgh\sin\theta +hF\qquad\hbox{se}\qquad \frac{d\theta}{dt} \lt 0. \end{equation}Queste due equazioni si possono riportare ad una forma più compatta se utilizziamo la funzione segno definita come
\begin{equation} \textrm{sgn}\biggl(\frac{d\theta}{dt}\biggr)=\cases{+1,&se \(d\theta/dt\geq 0\)\cr\\ -1&se \(d\theta/dt\lt 0\)\cr} \end{equation}per cui, dopo aver diviso per \(I_O\), entrambe si riducono alla
\begin{equation} \alpha= -\frac{mgh}{I_O}\sin\theta -\frac{hF}{I_O}\, \textrm{sgn}\biggl(\frac{d\theta}{dt}\biggr). \end{equation}Esplicitando il momento d'inerzia otteniamo l'equazione \begin{equation} \alpha= -\frac{mgh}{m(h^2+L^2/12)}\sin\theta -\frac{hF}{m(h^2+L^2/12)}\, \textrm{sgn}\biggl(\frac{d\theta}{dt}\biggr) \end{equation} che, riprese le definizioni di velocità angolare e di lunghezza efficace \eqref{eq:eq07}, e definito l'ulteriore coefficiente positivo \begin{equation} c=\frac{hF}{m(h^2+L^2/12)} \end{equation} giungiamo, in definitiva, all'espressione \begin{equation}\bbox[border:1px solid red,15px,#ffffcc] {\alpha= -\frac{g}{l_{eff}}\sin\theta -c\,\textrm{sgn}(\omega).}\label{eq:eq17} \end{equation} che costituisce il punto di partenza dell'analisi numerica nel caso di attrito radente.
Seconda pagina.
Continua alla pagina seguente.