La concoide di Nicomede
- Notizie storiche
- Definizione di concoide
- Concoide di Nicomede ed equazioni rappresentative
- Costruzione
Notizie storiche
Nicomede, antico scienziato greco del secondo secolo a.C., introdusse la curva che egli chiamò concoide (conchiglia in greco) per la soluzione grafica del problema della divisione di un dato angolo in tre parti uguali ossia della trisezione dell'angolo. Oggi sappiamo che questo problema si risolve con riga e compasso solo per alcuni angoli ma non per tutti. Tuttavia il problema si risolve ricorrendo ad altre curve, in particolare alla concoide.
Definizione di concoide
Una curva concoide è un insieme di punti del piano che si ottiene a partire da una curva piana \(f\) data (detta anche curva base) seguendo la costruzione descritta di seguito.
Figura 2.1. concoide01.ggb.
In riferimento alla figura 2.1,
- quale curva base scegliamo la parabola di equazione \(f\colon x=a y^2+2\) (curva di colore rosso) dove il coefficiente \(a\) del termine di II grado è associato ad uno slider il cui valore iniziale è, in figura 2.1, pari a \(-4.4\) ma che successivamente potremo variare.
- Sia O un punto qualsiasi (detto polo) e c una retta del fascio proprio con centro in O . Questa interseca in A la curva base.
- Se ora costruiamo una circonferenza di centro A di dato raggio (anche in questo caso tale grandezza è associata ad uno slider di valore iniziale \(0.9\),
- l'intersezione di questa con la retta definisce i punti B e C della retta c.
Il luogo geometrico dei punti B e C al variare della retta c passante per il polo e tali che \(AB=AC\) costituisce la curva concoide associata alla curva \(f\) data e al polo scelto. Nella costruzione questi luoghi appaiono in colore blu: in particolare la parte descritta dal punto più lontano dal polo individua il ramo esterno della concoide mentre l'altra parte, descritta da C definisce il ramo interno.
Concoide di Nicomede ed equazioni rappresentative
Nel caso che la curva base sia una retta la concoide associata viene detta concoide di Nicomede. Per ottenere la sua equazione cartesiana che lega le coordinate \(x,y\) dei punti B o C scegliamo
- il polo nell'origine del sistema cartesiano xOy,
- la curva base sia la retta c parallela all'asse y ed espressa dall'equazione \(x=k\),
- mentre sia \(AB=AC=r\) il raggio della circonferenza che determina B e C su c.
Per osservarne la forma nel caso sia \(O(0,0),\ k=2,\ r=1\) basta riportare il parametro a nella precedente figura 2.1 al valore nullo cosicché la parabola degenera in una retta parallela all'asse y.
Figura 2.2. concoide02.ggb.
Allo scopo di ottenere l'equazione cartesiana, sia \(y=m x\) l'equazione del fascio di rette per O. Poiché questa è l'equazione soddisfatta dal punto \(A(k,t)\) con \(t\) parametro che individua la generica ordinata di A e, ovviamente da \(B(x,y)\) e \(C(x,y)\), l'appartenenza di A a tale retta implica che i parametri \(m\) e \(t\) siano legati dalla \(t=m k\). Nella deduzione che segue utilizzeremo comunque il parametro \(m\). Per B (o C) il coefficiente angolare \(m\) si può esprimere anche come \begin{equation}m={y_B-y_A\over x_B-x_A}={y-t\over x-k}\quad\Rightarrow\quad y-t=m(x-k).\label{eq:2}\end{equation}
D'altra parte la condizione \(AB=r\) si traduce in \begin{equation}AB^2=r^2\quad\Rightarrow\quad (x-k)^2+(y-t)^2=r^2\label{eq:3}\end{equation} per cui sostituendo la \eqref{eq:2} nella \eqref{eq:3} abbiamo \begin{equation}(x-k)^2+m^2(x-k)^2=r^2\quad\Rightarrow\quad (x-k)^2(1+m^2)=r^2.\label{eq:4}\end{equation} Volendo eliminare la dipendenza dal parametro m sostituiamo ad \(m\) l'espressione \(m=y/x\) per cui \begin{equation}(x-k)^2\biggl[1+\biggl({y\over x}\biggr)^{\kern-2pt 2}\biggr]=r^2\quad\Rightarrow\quad (x-k)^2\biggl(1+{y^2\over x^2}\biggr)=r^2 \quad\Rightarrow\quad (x-k)^2\cdot{x^2+y^2\over x^2}=r^2.\end{equation} La moltiplicazione per \(x^2\) permette di ottenere infine quanto cercato cioè l'equazione rappresentativa \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{(x-k)^2(x^2+y^2)=r^2 x^2.}\label{eq:5}\end{equation}
La forma parametrica si ottiene invece dalla \eqref{eq:4} \begin{equation}(x-k)^2(1+m^2)=r^2\quad\Rightarrow\quad (x-k)^2={r^2\over 1+m^2}\end{equation} da cui considerando la radice quadrata dei due membri \begin{equation}|x-k|={r\over\sqrt{1+m^2}}\quad\Rightarrow\quad x=k\pm {r\over\sqrt{1+m^2}}.\end{equation} Utilizzando per l'ordinata \(y=mx\) e sostituendovi il risultato precedente si ha
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=k\pm {r\over\sqrt{1+m^2}}\cr\cr y=mk\pm {mr\over\sqrt{1+m^2}}}}\label{eq:9}\end{equation}Se ricordiamo che il coefficiente angolare di una retta esprime pure la tangente goniometrica dell'angolo \(\theta\) che tale retta definisce con l'asse x ossia \(m=\tan(\angle FOC)=\tan\theta\) (fig. 2.2), nonché le ulteriori identità goniometriche \begin{equation}\sin\theta={\tan\theta\over\sqrt{1+\tan^2\theta}}={m\over\sqrt{1+m^2}},\qquad \cos\theta={1\over\sqrt{1+\tan^2\theta}}={1\over\sqrt{1+m^2}}\end{equation} allora la \eqref{eq:9} diviene
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=k\pm r\cos\theta\cr y=k\tan\theta\pm r\sin\theta}}\end{equation}
Se invece il sistema di riferimento è un sistema polare (O il polo e Ox l'asse polare), l'equazione polare si ottiene osservando che (fig. 2.2) \begin{equation}{OF\over OA}=\cos\theta\quad\Rightarrow\quad OA= {OF\over\cos\theta}={k\over\cos\theta}\end{equation} per cui le coordinate polari di B e C saranno rispettivamente
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\rho_B=OB=r+OA=r+{k\over\cos\theta}\qquad \rho_C=OC=-r+OA=-r+{k\over\cos\theta}.}\end{equation}
Costruzione
I possibili passi e gli strumenti utilizzati per la costruzione di tale curva con GeoGebra sono:
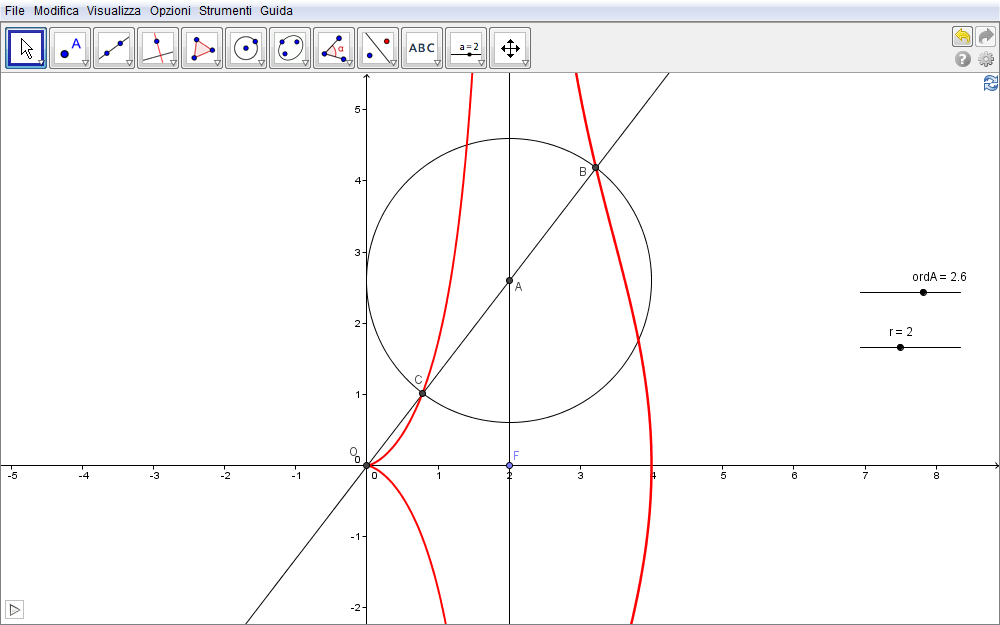
Figura 2.3. concoide03.ggb.
- Tracciare la retta per i punti O e F (rinominati in coerenza con le figure precedenti);
- costruire la retta perpendicolare a questa passante per F.
- Inserire lo slider che rappresenterà l'ordinata del punto A definendo i suoi valori estremi (nella costruzione tra -10 e 10): nell'applet lo si è nominaro ordA.
- Definire nella barra di inserimento il punto \(A(2,\)ordA\()\) e
- inserire lo slider r che rappresenta il raggio della circonferenza centrata in A (r varierà tra 0 e 5).
- Ora con lo strumento Circonferenza-dati centro e raggio
 tracciare la circonferenza di centro A e raggio pari ad r.
tracciare la circonferenza di centro A e raggio pari ad r.
- Costruire la retta per O e A.
- Definire le intersezioni B e C della retta OA con la circonferenza ed infine
- richiedere la visualizzazione del luogo dei punti B al variare dello slider ordA.
- Analogamente per il punto C.
Siamo ora in grado, variando il raggio r, di evidenziare alcune caratteristiche di tale curva:
- la forma della concoide è sempre simmetrica rispetto alla retta OF (nel nostro caso l'asse x);
- la retta base FA è un asintoto sia per il ramo esterno che per il ramo interno;
- la forma del ramo interno della concoide dipende essenzialmente dal rapporto fra i due parametri k e r ossia tra le lunghezze dei segmenti OF e il raggio \(AB=AC=r\) della circonferenza. In particolare,
- quando r > k (nel nostro caso r > 2) il ramo interno ha un cappio e il polo è un nodo;
- quando r = k, il cappio del ramo interno si riduce al polo e forma una cuspide;
- quando r < k il ramo interno non passa per il polo e quest'ultimo è un punto isolato della curva in quanto le sue coordinate, nell'esempio \(O(0,0)\), soddisfano comunque l'equazione \eqref{eq:5}.
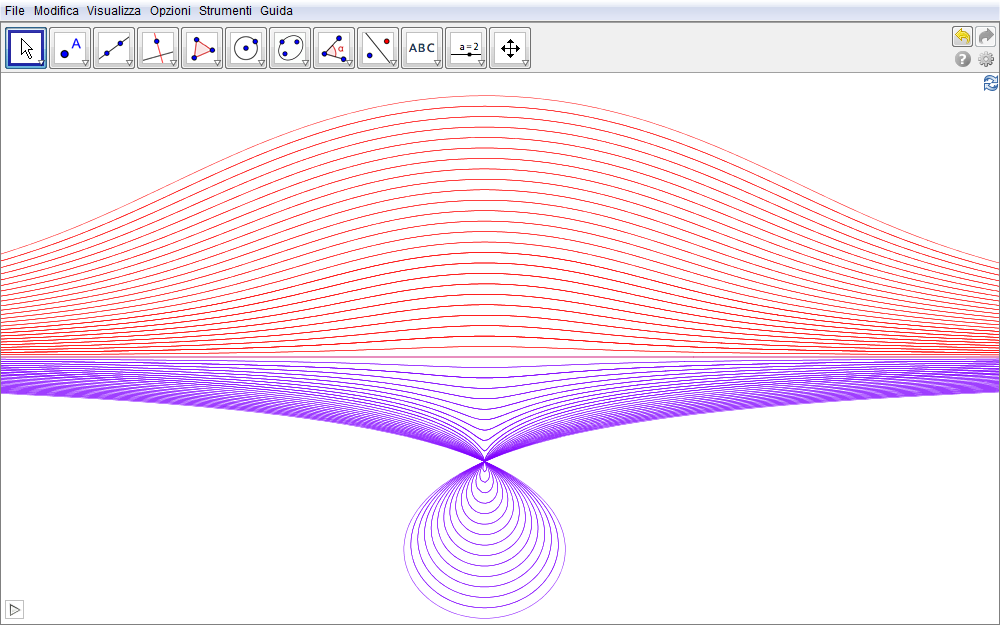
Attivando l'animazione nella figura sottostante (dedotta dalla precedente scambiando le coordinate del punto A in modo che questo vari su una retta parallela all'asse delle ascisse) si ottiene al variare del parametro r una famiglia di concoidi dove ciascuno dei due rami è rappresentato dal medesimo colore.
Figura 2.4. concoide04.ggb.
Nella successiva fig. 2.5 invece si intende distinguere con un diverso colore le concoidi descritte dal ramo interno e da quello esterno.
Figura 2.5. concoide05.ggb.