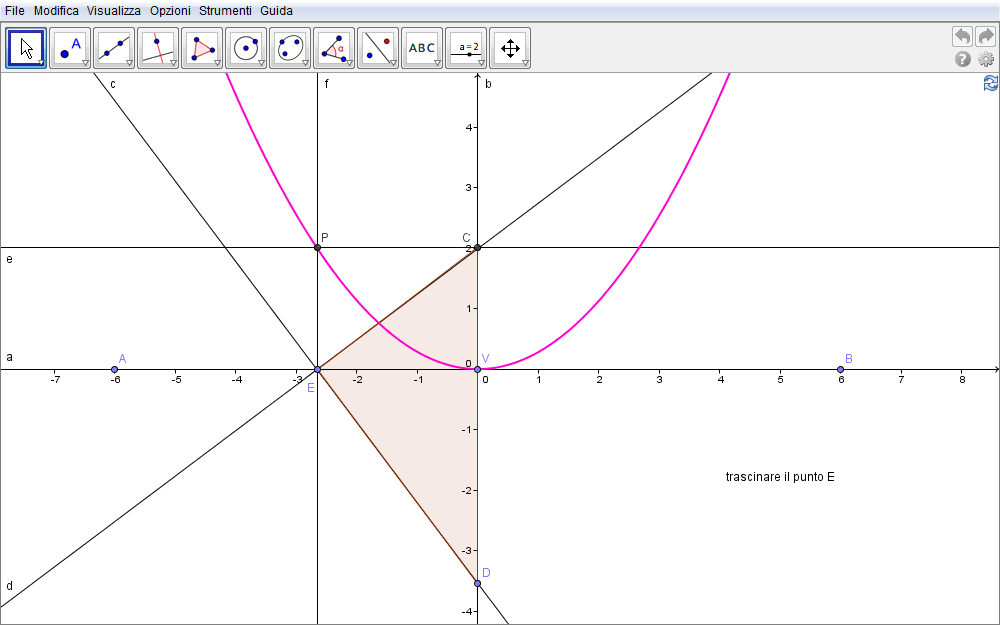
Parabola: costruzione n. 2
La seconda costruzione della parabola parte fissando due punti, il primo nell'intersezione di due rette perpendicolari sarą il vertice della parabola, il secondo apparterrą ad una di queste due rette.
- Tracciata la retta (orizzontale) a (fig. 1.4),
- si prenda su di essa un punto V (sarą il vertice della parabola) e
- si costruisca la retta b perpendicolare ad a per V (sarą l'asse della parabola).
- Definito su b un punto D sia
- E un punto qualsiasi di a.
- Si tracci ora la retta DE.
- Perpendicolarmente a questa si costruisca l'ulteriore retta d passante per E e sia
- C il suo punto di intersezione con b.
- Tracciate le perpendicolari per C a b e
- per E ad a,
- queste si incontrano nel punto P il cui luogo, al variare di E è la parabola di vertice V e asse b.
Figura 1.4. parabola04.ggb.
In questa costruzione appare in modo esplicito sia l'asse della parabola sia un punto importante appartenente alla parabola stessa, il punto V, cioè il suo vertice. Il fuoco invece non è coinvolto in tale costruzione. La dimostrazione che riportiamo presuppone sia nota l'equazione cartesiana della parabola con vertice nell'origine come quella ottenuta nella pagina precedente ossia, in generale, \(y=k x^2\).
Difatti se consideriamo le rette a e b come gli assi di un sistema cartesiano con origine in \(V(0,0)\) e poniamo \(P(x,y)\) per cui le coordinate dei punti E e C saranno \(E(x,0)\), \(C(0,y)\) e posto \(D(0,d)\), il secondo teorema di Euclide applicato al triangolo rettangolo EDC assicura che \begin{equation}EV^2=DV\cdot VC\quad\hbox{da cui}\quad x^2=\bigl|\,d\,\bigr|\,y\quad\Rightarrow\quad y={1\over \bigl|\,d\,\bigr|}x^2\end{equation} che rientra nella equazione canonica appena ricordata. Dal confronto con essa discende che l'ordinata \(f\) del fuoco \(F(0,f)\) della parabola associata al punto D deve soddisfare alla relazione \(4f=\bigl|\,d\,\bigr|\) cioè \(f=(1/4)\bigl|\,d\,\bigr|\).